Paper in Phys. Rev. Lett. on explaining the bump in the avalanche distribution

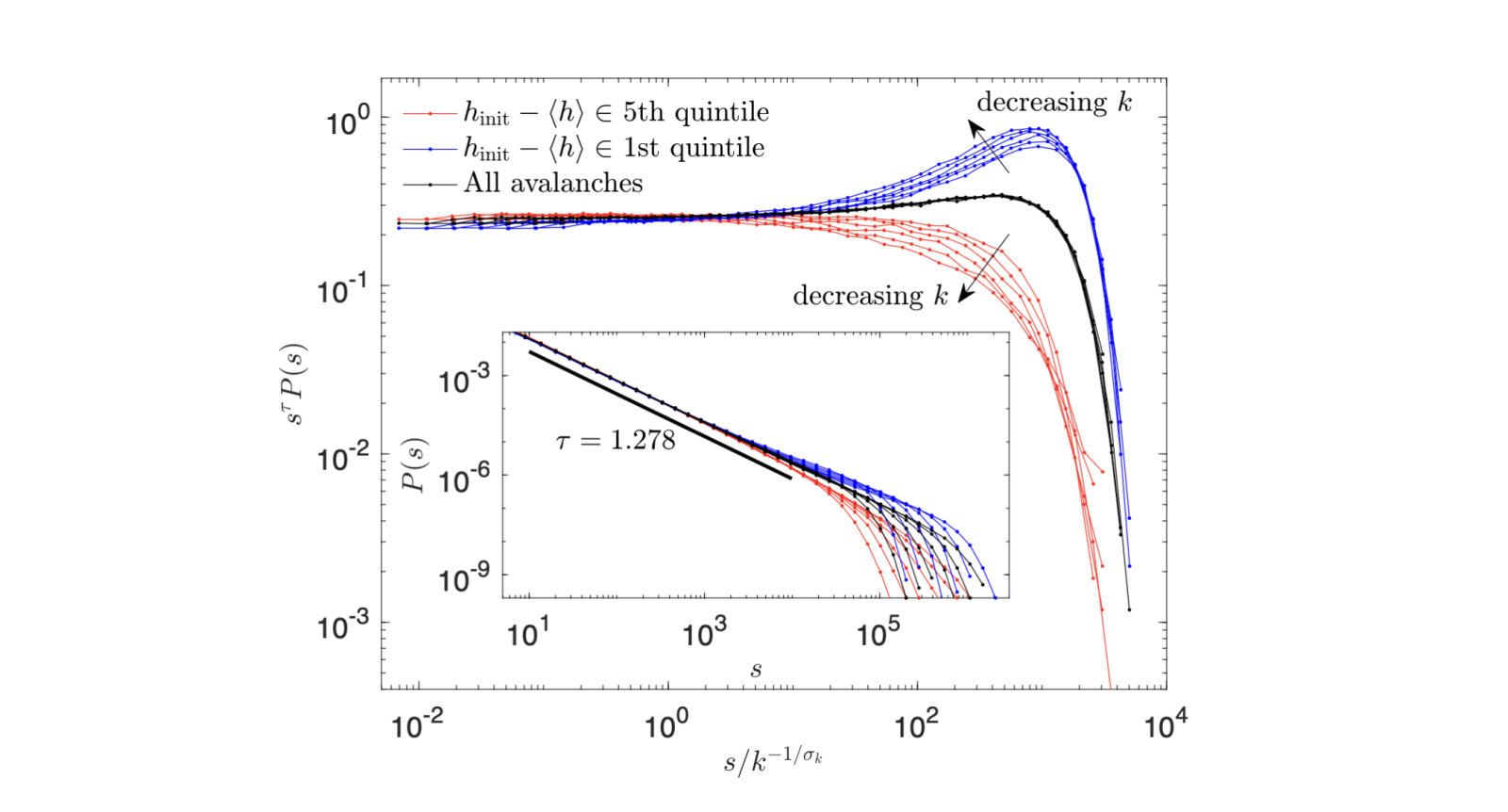
Abstract: The depinning transition critical point is manifested as power-law distributed avalanches exhibited by slowly driven elastic interfaces in quenched random media. Here we show that since avalanches with different starting heights relative to the mean interface height or different initial local interface curvatures experience different excess driving forces due to elasticity, avalanches close to the “global” critical point of non-mean-field systems can be separated into populations of subcritical, critical, and supercritical ones. The asymmetric interface height distribution results in an excess of supercritical avalanches, manifested as a “bump” in the avalanche size distribution cutoff.