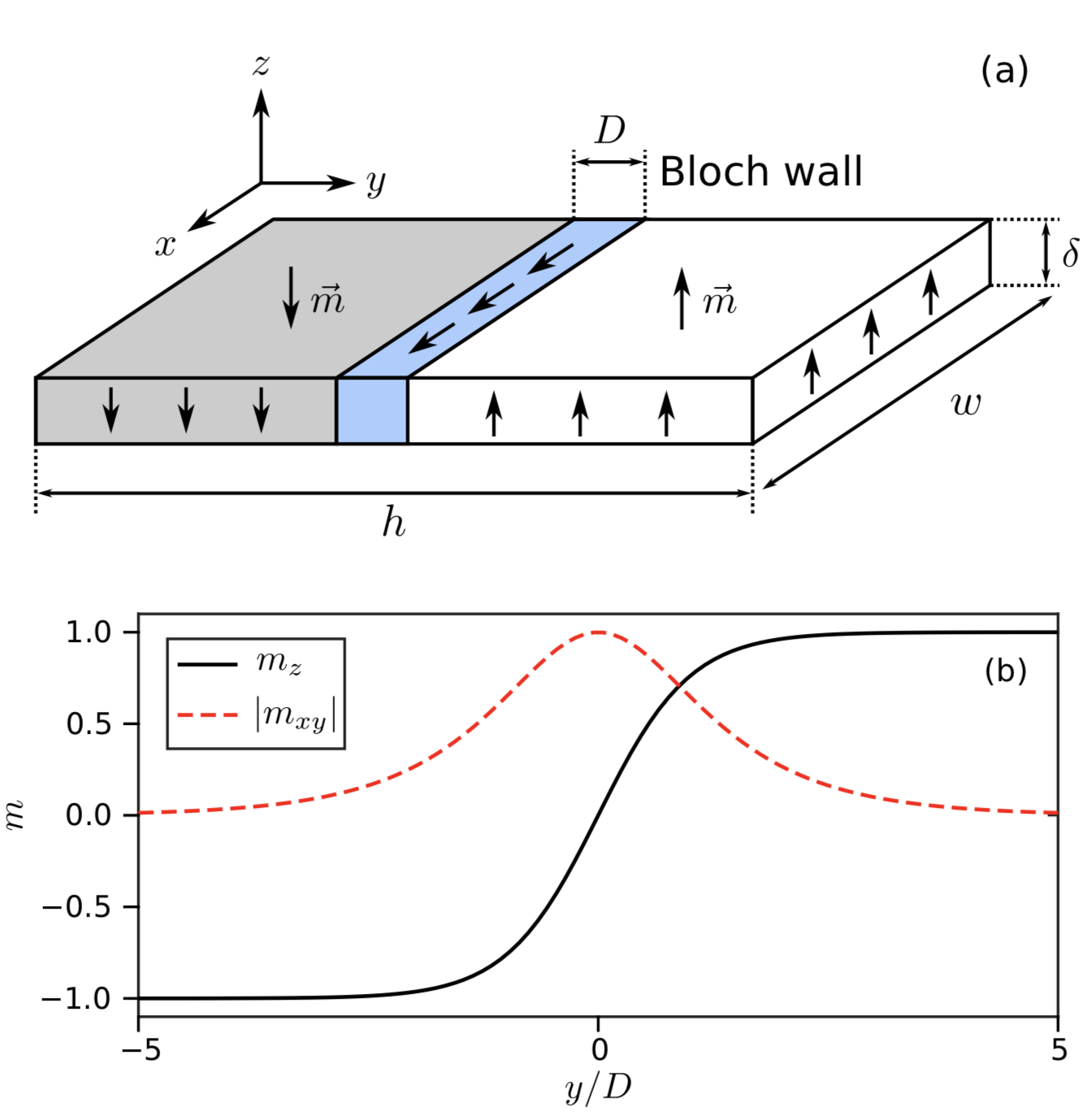
Due to its nonlocal nature, calculating the demagnetizing field remains the biggest challenge in understanding domain structures in ferromagnetic materials. Analytical descriptions of demagnetizing effects typically approximate domain walls as uniformly magnetized ellipsoids, neglecting both the smooth rotation of magnetization from one domain to the other and the interaction between the two domains. Here, instead of the demagnetizing field, we compute analytically the demagnetizing energy of a straight domain wall described by the classical tanh magnetization profile in a thin film with perpendicular magnetic anisotropy. We then use our expression for the demagnetizing energy to derive an improved version of the 1D model of field-driven domain wall motion, resulting in accurate expressions for important properties of the domain wall such as the domain wall width and the Walker breakdown field. We verify the accuracy of our analytical results by micromagnetic simulations.
Audun Skaugen, Peyton Murray, and Lasse Laurson, Analytical computation of the demagnetizing energy of thin film domain walls, Phys. Rev. B 100, 094440 (2019).