Projects

We work on a number of different topics crossing boundaries between statistical physics, materials science and machine learning. We are especially interested in non-equilibrium collective phenomena in materials, such as the critical-like avalanche dynamics occurring in various driven systems. Some examples of our current and recent research are given below.

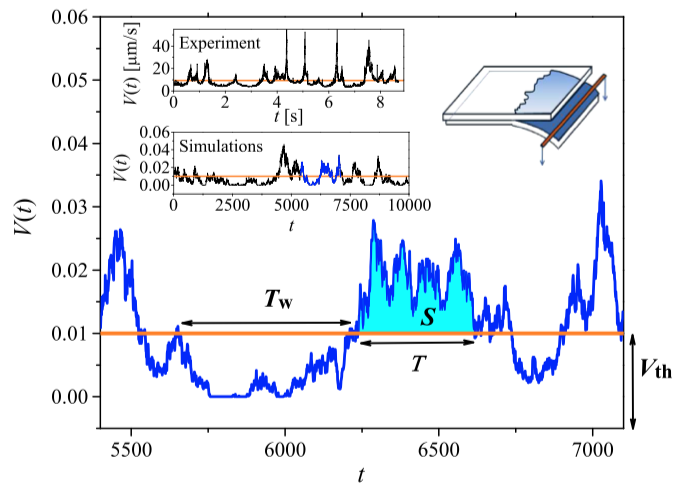
Domain wall dynamics in ferromagnets

The study of domain wall dynamics in ferromagnets encompasses several core ideas of modern theoretical physics, including topology and non-equilibrium statistical physics. Here, we focus on theoretical and numerical studies of dynamics of domain walls in various low-dimensional ferromagnetic structures such as thin films, nanowires and -strips. The key issues to be addressed are the effects of structural disorder and thermal fluctuations on the domain wall dynamics, driven by either applied magnetic fields or spin-polarized electric currents. The study relates in particular to fundamental theoretical questions in modern statistical physics of elastic interfaces in random media, and has also important practical implications for the operation of next generation memory and logic devices based on domain walls. Until the end of 2019, these activities were pursued via the Helsinki Institute of Physics (HIP) Theory Programme project “Domain wall dynamics”.

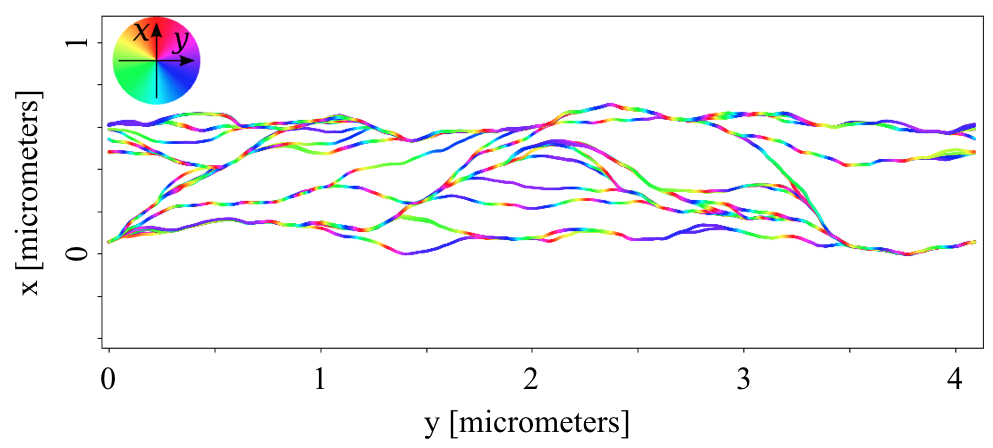
Micromagnetic simulations of domain wall in a disordered ferromagnetic thin film with perpendicular magnetic anisotropy, with the domain wall moving from bottom to top. The figure shows the domain wall configurations in-between the Barkhausen jumps, the “crackling noise” events exhibited by moving domain walls in disordered ferromagnets. The domain wall is moving in the precessional regime and hence contains Bloch lines, i.e., localised regions where the chirality of the domain wall changes, visible in the figure as abrupt changes of colour, representing the orientation of the internal in-plane domain wall magnetisation. Check out our related recent paper Phys. Rev. Lett. **122**, 117205 (2019). (figure by Touko Herranen).

Plastic deformation of crystals

In contrast to the traditional paradigm of a smooth flow-like process, plastic deformation of crystalline solids has recently been found to have a wildly fluctuating and bursting character, originating from the collective stress-driven motion of interacting dislocations, the line-like topological defects of the crystal lattice. This complexity poses one of the greatest current challenges in non-equilibrium physics in that many important empirical observations remain unexplained. This calls for novel approaches to understand the underlying fundamental physics and creates the exciting prospect of optimising the mechanical properties of materials by controlling the dislocation dynamics.

Here our aim is to gain new insights on the complexity and collective effects such as strain bursts statistics in crystal plasticity via discrete dislocation dynamics simulations. Recently, we have also started to exploit machine learning in order to predict and optimise the plastic deformation process of crystals. Starting in September 2019, these activities will be pursued via the Academy Project Complexity and optimization in crystal plasticity (COPLAST), funded by the Academy of Finland.

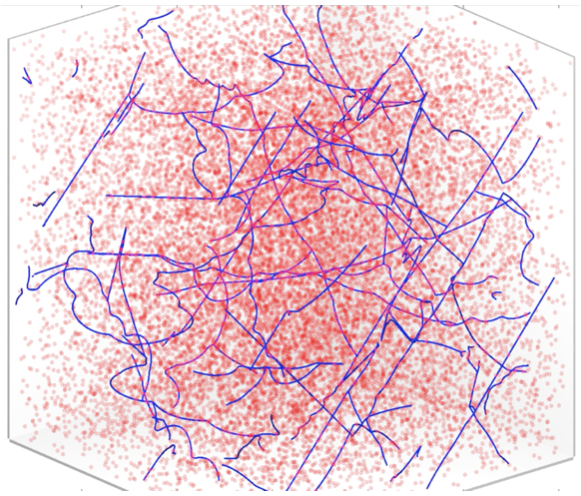
Three-dimensional discrete dislocation dynamics simulations of crystal plasticity using the ParaDis code. The stress-driven motion of dislocations (blue lines) mediates the plastic deformation process of the crystal. The red dots represent precipitate particles interfering with dislocation motion, making the material stronger. Here, we aim at both understanding the fundamental nature of the collective dynamics of dislocations and developing methods based on machine learning to predict and optimise the deformation process. For an example on the latter, check out our recent paper Nat. Commun. 9, 5307 (2018). (figure by Arttu Lehtinen).

Crack propagation in solids

Cracks propagating in disordered solids constitute one of the key examples of systems exhibiting crackling noise, i.e., bursty and intermittent response of the system to slow external driving. We use numerical models of cracks such as long-range elastic strings in random media to study the statistical properties of the bursty crack front dynamics, often in close collaboration with experimentalists (Stephane Santucci, ENS Lyon).