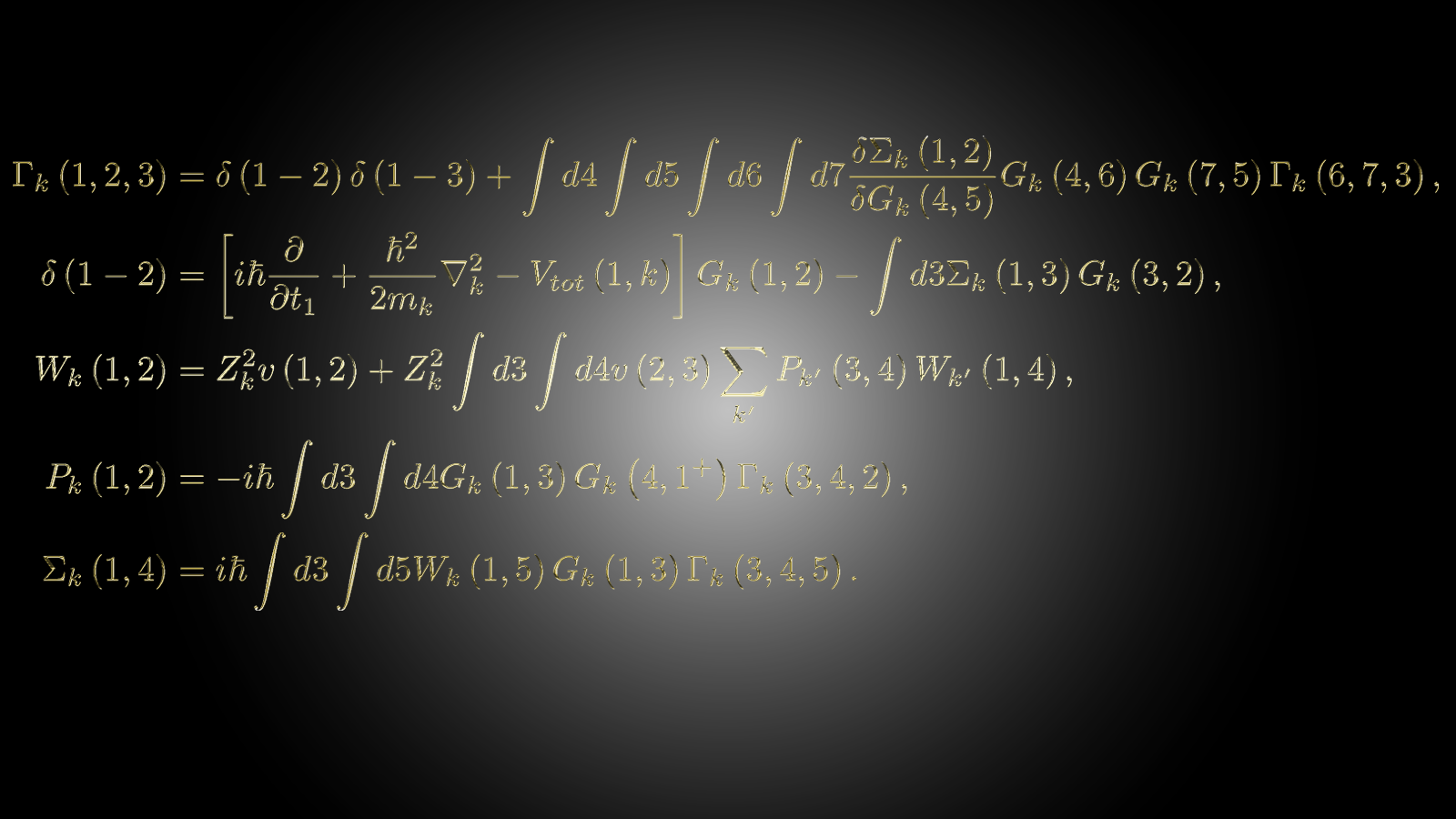In the description of molecules and solids, the nuclear degrees of freedom are conventionally treated in first quantization and the identical nuclei are treated as distinguishable. There is a justified reason for that, namely, the nuclei in molecules and solids are usually rather well localizes near their equilibrium positions and the neglect of (anti)symmetrisation will not make a significant error. This is not, however, necessarily true in some extreme cases like quantum crystals.
In the quantum field theoretic approach developed here, the only assumption is the Hamiltonian of Coulomb interaction. It does not suffer from the same limitations as the first quantized version with the approximate treatment of nuclear variables. Even though, the general form of this theory cannot be implemented in practice, we are hopeful that in some cases this approach, in its approximate form, might be useful in the description of some extreme cases like quantum crystals.
The developed theory can be formulated in the language of non-relativistic quantum field theories. Namely, starting from the action, with the Lagrangian written in terms of the so-called Schrödinger fields. Among the main results obtained here are the exact equations of motion, which can be written in the form of Hedin’s equations for all species of particles.